Let me tell you – I am incredibly thrilled to have this Konica Hexanon AR 57mm f1.2. More so, because I bought it by chance – saw a good deal on eBay and took it, hoping it would turn out to be a good one. I was not wrong! This lens turned out to be exceptional in a lot of ways. First of all – it is the most radioactive lens that I own, peaking at over 37,000 counts per minute. Secondly, it produces some of the most striking images – detailed, sharp, with silky bokeh. It’s not cheap, especially compared to other Konica lenses, but it is still less expensive than the other fast lenses.

Build quality and construction
This lens is like a tank — robust and hefty piece of Japanese engineering featuring world-class glass. One look at the imposing front element proves this lens means business. Konica Hexanon AR 57mm f1.2 was at the top of the standard lens lineup, aimed at professional use. And it shows.
The rear element is unique – part of the glass is cut to accommodate the aperture pin. Similar to the Tomioka 55mm f1.2, but in a straight line instead of a curve. The cut-off shape can show up in the bokeh, if the lighting is right, which might be a potential issue for some people.
Aperture has half stops, making it easy to get the desired value. Blades are snappy and well made. The ring is not too damped, and can feel a little loose – it’s easy to go too far when changing the aperture.
I prefer a focal length which is slightly longer than 50mm for a standard lens. In this case, 57mm is just right for me. Focusing is easy, and smooth – there is ample sharpness to show the clear plane of focus using the focus peaking. Some softer lenses don’t trigger the peaking, and they are never truly sharp, especially wide open.



Image quality
I can’t take this lens off the camera! Figuratively – in reality, I take it off after shooting to protect the camera’s electronics, as the lens is quite radioactive. The thorium in the lens irradiates the images with life. A subtle yellowing of the elements acts as a warm filter. Some people decide to ‘de-yellow’ the thorium glass, but I prefer to keep it. There is plenty of clear modern glass on the market and only a few warmly glowing thoriated lenses from the bygone era. Nobody makes them anymore, except for the military.
Even the weird cut-off bokeh shape does not bother me too much. There are other lenses for that sort of photography, where the bokeh becomes the main subject. Konica Hexanon AR 57mm f1.2 is not suited for that type of photography unless you want to see the cut-off circles for some reason. However, it manages to blend the background into a smooth soup of colour in a very pleasing way when there are no highlights.
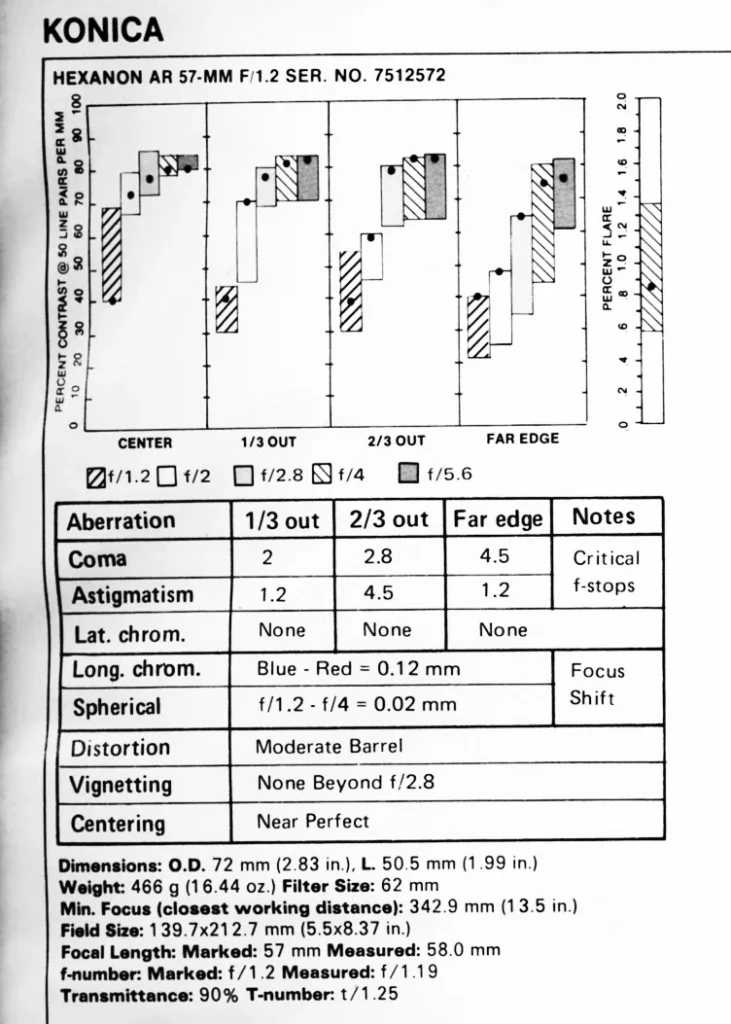
Image quality wide open is pleasing – acceptably sharp, albeit a little on the softer side. OK for portraits, but could be too soft for other subjects. Sharpness improves dramatically in the centre of the frame from about f2.8, while still retaining the excellent bokeh rendering. From f4 most of the frame is pin-sharp. Most of my photos are within this range unless I need a more significant depth of field.
So yeah, to sum it up – I appreciate the images this lens produces time and time again.

Adapting Konica Hexanon AR 57mm f1.2 to Mirrorless
Konica AR mount flange distance limited the usage of the excellent Konica glass on a modern DSLRs. Flange distance was way shorter than Canon or Nikon, which meant there is no space remaining for the adapter. Konica lenses would either need special corrective adapters which I am unsure ever existed. And without a viable adapter, Konica lenses would either not focus to infinity or even hit the camera’s mirror.
Luckily, that is no longer the case, and we can readily adapt the Konica AR lenses to most mirrorless cameras, like my Canon EOS R.
I use a Fotasy Konica AR to EOS RF mount adapter. It was affordable – cost about 20 USD from Amazon USA. The quality is excellent, though – there is absolutely no play between the lens and the adapter, or the adapter and the camera. Everything is snug and firm. Exactly what you need when mounting a precious lens such as this.

Radiation
Konica Hexanon AR 57mm F1.2 is radioactive – more than all other lenses measured. A reading of the lens’ front is about 37,662 CPM and 26,000 CPM at the back. Typically, lenses have thoriated elements either at the front or at the back of the lens, unlike Konica Hexanon AR 57mm f1.2, which is radioactive from both ends. Thorium is added intentionally to improve the optical properties of the glass. Konica even boasted about it in their promotional material.
Not the least important is the production of several types of optical glass, many of which embody rare earths. Exotic elements such as Thorium, Lanthanum and Zirconium are added to glass mixtures to create the high refractive indexes necessary in sophisticated lens designs. Selection of premium quantities of glass from the large glass pots, stringent spectrophotometric tests after stress and strain checks provide the valuable raw glass for ultimate use in lens elements.
– KONICA HEXANON LENSES FOR AUTOREFLEX CAIVIERAS, Konica Camera Company, 1972.
Apart from a few precautions, radioactive lenses are generally safe to use, after all – they are consumer devices. You can read my article about radioactive lenses to find out more.


Price and availability
Bought for £450 from eBay UK. You can also find it for about €500 on eBay DE, and $600 on eBay USA. Look around, and be prepared to wait a litte until you find one appropriately priced. It is not too rare, but finding one in a good condition for the acceptable price can be a little difficult.
Similar lenses
Conclusion
What a lens! Konica Hexanon AR 57mm f1.2 ticks all my boxes and I don’t intend to sell it. I prefer the images taken with it over a lot of other vintage lenses. Must be the thorium! This lens is a 5 / 5 for me.
Have you used Konica Hexanon AR 57mm F1.2? Let me know what you think about this review and leave a comment!
Sample Images










Leave a Reply